[배상면*수학강사]

인류 역사상 가장 위대한 과학책이자 수학책은 이건 반박 불과 딱 두 권입니다.
하나는 유클리드의 <유클리드 원론> 기원전 300년에 쓰여진 책이고요. 또 하나는 뉴턴의 <프린키피하>입니다.
이것 말고도 위대한 과학책 많잖아요. 물론 많죠. 그러나 우리는 <유클리드 원론>과 <프린키피아>가 쓰여진 서술방식에 주목할 필요가 있습니다. 여기에는 다른 책들과 다르게 ‘공리’라는 게 등장하는데요.

10개의 법칙으로 수학을 설명한 유클리드
<유클리드 원론>은 공리가 딱 10개 나옵니다. 그리고 수학 전체를 공리 열 개만 가지고 서술을 하고 있죠. 그래서 수학자 과학자들이 어린 시절에 <유클리드 원론>을 접하고 ‘수학이 이런거야?’ ‘뭐 이런 미친 책이 다 있지?’ 이러고는 수학에 빠져서 나중에 수학자, 과학자로 성장하는 기반이 됩니다. 뉴턴이 그랬고, 버트런드 러셀, 아인슈타인 그리고 링컨 대통령도 심지어 그러했죠.

그럼 도대체 이 ‘공리’라는 것이 뭐냐? 그냥 열 개만 믿으면 수학이 다 된다는 겁니다.
예를 들어서 ‘A=B’에요. 이 등식에 양변의 C를 더하게 되면 ‘A+C=B+C’가 되죠. 당연한 거죠. 수학은 이렇게 등식의 양변에 같은 숫자를 더하거나 빼거나 곱하거나 나누어도(물론 영으로 나누는 걸 제외 했을 때) 등식이 유지가 됩니다.
그런데 잘 생각해 보시면 일차방정식 ‘2x+3=0’을 풀 때 양변에 ‘-3’을 더합니다. ‘2x=-3’ 양변에 1/2을 곱하면 ‘x=-2/3’이라는 답이 <유클리드 원론>에 있는 10개의 공리만 믿으면 굳이 일차방정식, 이차방정식, 학원 다니면서 배우지 않아도 원론적으로는 다 된다는 얘기죠.
이게 얼마나 무시무시하냐면요. 예를 들어서 김연아 선수가 피겨 교과서를 썼어요. 책이 엄청 두꺼워요. 근데 거기에 서론에 ‘피겨는 딱 3개만 하면 돼. 주행할 때는 정면을 봐. 점프할 때 허리 펴고, 회전할 때는 고개를 먼저 던져’ 이랬다고 합시다. 참고로 저는 피겨의 ‘피’자도 모릅니다. 그런데 거기에 등장하는 피겨의 기술들이 1,000개예요. 그런데 그 1,000개가 이 세 가지만 지키면 다 돼요. 그래서 이 세 가지 원칙을 가지고 1,000개의 동작을 따라 했더니 나도 프로 피겨선수가 되더라. 이러면 엄청난 거 아닙니까? 이런 식의 서술을 방식이 공리적 서술 방법이에요.
만유인력의 법칙, 뉴턴
놀라운 건 뉴턴의 <프린키피하>도 공리라는 걸 제시하고 있습니다. 예를 들면 ‘물체는 힘을 받으면 힘을 받은 만큼 비례해서 움직인다’라는 것, 속도의 변화가 생긴다는 거죠. 이걸 ‘f=ma’이라는 수식으로 나타낼 수 있습니다.

그래서 오늘날 뉴턴의 공리 3개를 ‘뉴턴의 역학 법칙’이라고 하는데요. 이 <프린키피하>에 대해서는 열어보기 전까지는 단순하게 과학책이 아닐까라는 기대를 가지고 열게 됐는데, 딱 열어보면 그냥 수학책이에요. 그냥 수학책, 기하학 책입니다.
<프린키피하>에는 이런 내용이 나와 있죠. ‘지구는 수학적으로 따져 보니까 타원 궤도로 돌아와야만 하던데?’ 이게 <프린키피하>의 내용이에요. 그 이전의 책은 ‘관찰을 해보니까 타원궤도로 돌던데.’라는 귀납적 사고였다면, 뉴턴의 <프린키피하>는 ‘수학적으로 타원궤도로 돌아야만 맞는 거야. 자연은 이걸 따라야 해.’ 라고 말하고 있습니다.
그래서 <프린키피하>가 나온 이후에 어떤 변화가 생겼을까요? 사람들은 더 이상 종교를 믿지 않죠. ‘자연은 수학과 과학의 법칙에 따라서 움직여야 하는구나. 그래서 종교사, 전쟁사, 예술사를 반으로 쪼개라.’ 이건 상당히 어려운 질문입니다만, “수학과 과학사를 반으로 쪼개라.” 그러면 뉴턴 이전/이후로 나누는 건 아주 명확합니다. 뉴턴 이후에 수학, 과학의 시대가 열렸기기 때문에 오늘날 아이작 뉴턴이 가장 위대한 수학자 과학자로 평가받는 이유는 <프린키피하>에 있는 것이죠.
여기서 잠깐, 수학을 못하는 아이들의 특징
수학을 못하는 친구들의 특징이 있어요. 질문의 질이 떨어집니다. 만약에 수학을 정말 못하는 중1 학생이고, ‘일차방정식 2x+3=0를 풀어라’ 질문한다고 칩시다. 저에게 딱 가져와서 “몰라요. 풀어주세요.”라고 했다고 칩시다.

저는 이 친구에게 책을 덮고 “방금 문제가 뭐였지?”라고 역질문을 합니다. 전혀 기억하지 못합니다. ‘일차, 방정식, x’ 셋 중에 아무것도 나오지 않아요. 이 친구는 그냥 모르겠으니까 풀어달라고 해서 제가 푸는 걸 보고 따라 풀 생각이었던 거죠. 문제가 뭐였는지, 무엇을 구하는지도 관심이 없는 상태에서는 이 문제를 맞출 수가 없죠.
이럴 때 저는 “방정식이 뭐지? 무엇을 구하는 거지?” 라고 묻고 돌려보냅니다. 그러면 그 친구가 다시 또 한 번 질문을 해요. 하지만 저는 아까 <유클리드 원론>에서 이야기했던 공리. ‘등식의 양변에 똑같은 연산을 해도 등식은 변하지 않는다’만 알려주고 또 보냅니다. 이 친구가 몇 번 만져 보더니 답이 나오죠. 이와 같이 답을 내는 과정은 질문을 다듬는 과정입니다.
아까 과학사를 둘로 쪼갠 사람이 누구라고요? ‘아이작 뉴턴’입니다. 뉴턴 시절에도 코로나같은 게 있었죠. 그 시절에 페스트가 런던에 퍼지면서 케임브리지 대학 펠로우였던 뉴턴은 강제 휴학을 당하게 됩니다.
대부분 과학사는 이런 순간에 명장면을 만들어내죠. 뉴턴은 고향인 울즈소프 뒷동산에서 사색과 관찰의 시간을 보내면서 떨어지는 사과를 보고 다음과 같은 질문을 했다고 합니다. “사과는 왜 떨어지지?” 이건 오스트로피테쿠스했을 것 같은 질문 아닙니까? 뉴턴의 질문은 “사과는 떨어졌는데 달은 왜 안 떨어지지?”라는 질문이었다고 해요.
그런데 우리가 뉴턴의 수학 과학의 절대자처럼 생각하듯이 뉴턴 시절에도 여기에 대한 답을 제시했던 절대자가 있었습니다. ‘아리스토텔레스’였죠. 그는 이렇게 말했습니다. “사과는 지상에 있으니 안 떨어지고, 달은 천상에 있으니 떨어지지 않는 거야.” 뉴턴의 질문이 계속됩니다. “어디까지가 지상이고, 어디까지가 천상이지?” 지상과 천상의 기준을 공기, 빛 이런 걸로 한다면, 공기라는 게 지구에서 멀어지다가 어느 순간에 딱 없어지나요? 빛이라는 게 지구에서 멀어지다가 어느 순간 딱 없어지나요? 사실은 지상과 천상의 명확한 구분 기준은 없죠.
여기에서 뉴턴의 질문이 이렇게 바뀝니다. “혹시 사과도 떨어지는 거 아니야? 혹시 달도 떨어지는 거 아니야? 떨어진다는 건 뭐지? 당기는 거지? 아, 사과와 지구가 당기듯이 달과 지구도 당기는구나”라는 걸 알게 되죠. 이렇게 탄생한 법칙이 만물은 서로를 끌어당긴다. <만유인력의 법칙>인 것입니다. 뉴턴이 했던 위대한 일은 질문을 다듬었던거예요.
이진법의 아버지, 라이프니츠
뉴턴과 함께 미적분을 창시했던 라이프니츠의 이야기로 잠깐 가겠습니다.

라이프니츠는 30년 전쟁의 끝자락에 태어납니다. 이 전쟁은 어찌보면 최초의 국제 전쟁으로 평가받는 유럽을 폐허로 만든 전쟁이었죠. 태어나 보니 나라가 유럽 전체가 엉망이 되어 있는 겁니다. 이때 소년 라이프니츠는 ‘각 나라의 입장이 서로 달라 싸우고 있으니 세계를 통합할 알파벳을 만들 거야.’ 이런 훈민정음 서문 같은 기특한 생각을 하게 됩니다.
성인이 된 라이프니츠는 다방면에 엄청난 업적을 남기게 됩니다. 철학에서는 <모나드론>으로 근대 철학 합리론의 3대 거장 중 한 명이고요. 사칙연산이 가능한 계산기를 만들기도 했죠. 또한 수학사의 가장 위대한 업적 중 하나인 미적분을 만들었기 때문에 그의 명성이 유럽 전체에 퍼지게 되고요.
라이프니츠는 하노버에 도서관장, 베를린 학술원 원장으로 명성을 날리게 됩니다. 이때 그에게 엄청난 계기가 오죠. 선교사를 통해 중국의 <주역>을 접하게 됩니다. “아, 알파벳 찾았다!” 주역의 ‘괘’란 긴 막대 하나와 짧은 막대기 두 개로 정보의 단위를 만드는 것이었죠. 라이프니츠는 주역의 괘를 접하는 순간 0과 1 두 숫자의 조합으로 정보를 만들어 나가는 ‘이진법’을 생각하게 됩니다.
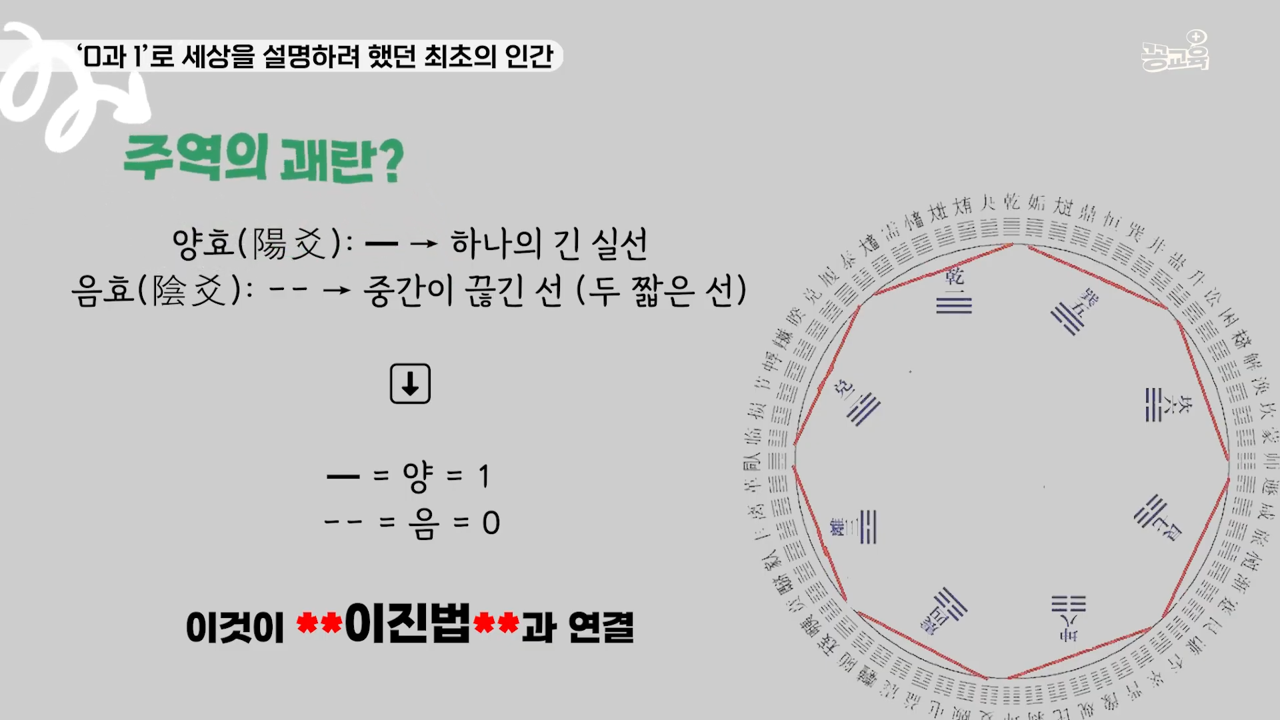
그리고 시간은 300년쯤 지나 1969년. 우리 인류는 달에 우주선을 보내게 되죠. 그런데 진짜 놀라운 건 우주선이 지구로 귀환하기 전에 달 사진을 보냈다는 겁니다. 어떻게 보냈을까요? 당시 아폴로 11호에는 최초의 우주인으로 불리는 암스트롱도 타고 있었지만 수학천재 버드 올드린이 타고 있었어요. 그들은 달 착륙사진을 작은 픽셀로 쪼개 다음에 한 픽셀마다 256개의 컬러를 지정합니다. 왜 256개일까요? 2에 여덟 제곱이 256입니다. 여덟 개의 칸을 만들어서 한 칸을 0또는 1을 배치하는 겁니다. 그래서 전부다 1이 쭉 들어가면 퓨어 화이트, 전부다 영이 쫙 깔리면 퓨어 블랙. 이렇게 256개의 컬러를 각 셀마다 지구로 전파로 쏴주는 거죠. 그리고 지구에서는 그 전파를 받아서 다시 색깔로 번역을 해서 사진을 완성했던 것이죠.
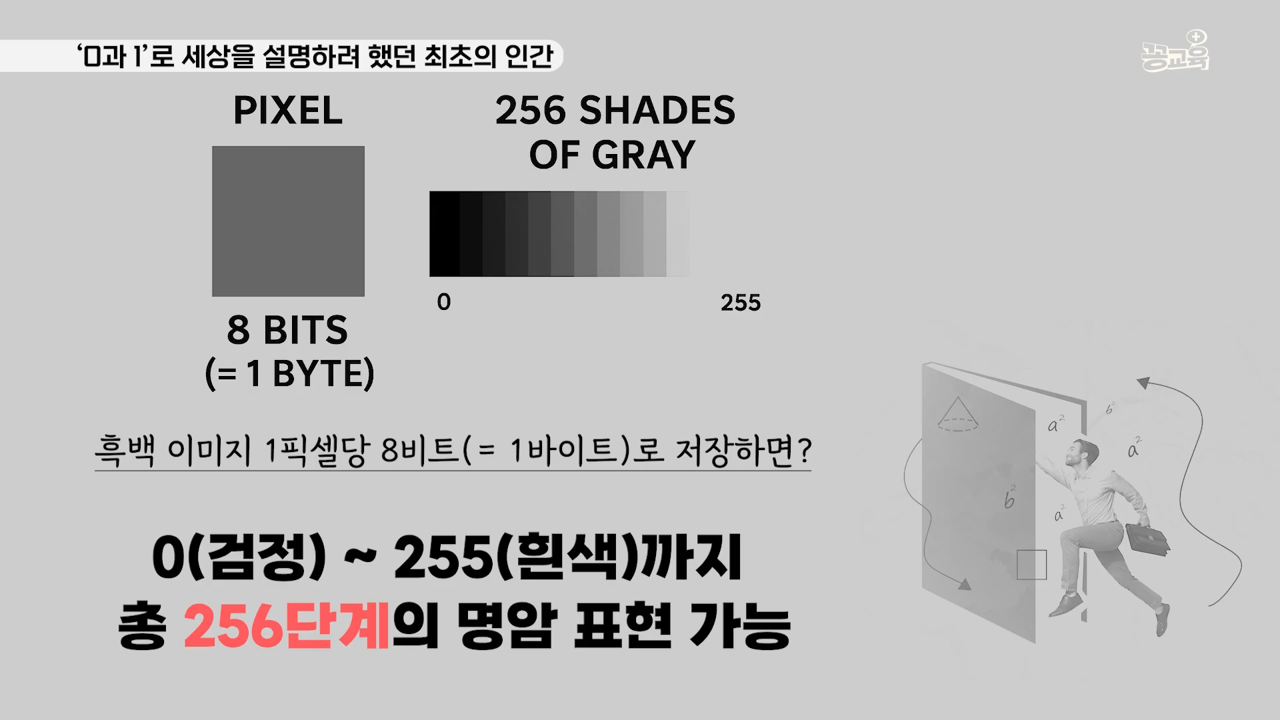
이렇게 라이프니츠가 있었기 때문에 이진법이 탄생했고, 디지털이라는 개념이 생기면서 자료를 사실상 수학으로 전송하게 될 수 있었던 것이죠. 뿐만 아니라 오늘날 컴퓨터의 알고리즘은 이진법으로 작동하죠. 컴퓨터는 전기 신호 온/오프 두 개를 가지고 모든 의미 전달을 다 해낼 수 있습니다. 라이프니츠가 이진법을 생각했던 덕분이고, 어린 시절에 훈민정음 서문 같은 생각을 했기 때문이죠.
안타깝게도 제가 어렸을 때 좋아했던 뮤지션들이 비틀즈, 퀸 이런 분들이에요. 이 분들의 영상을 지금 보면 약간 빛 바랜 영상이죠. 그런데 요즘 친구들은 몇 년 후, 아니 몇 천년 후에도 블랙핑크의 영상을 생생하게 볼 수 있을 겁니다. 디지털의 힘이죠. 라이프니츠 덕분입니다.
인공지능의 창시자, 앨런 튜링

또다른 분을 만나보죠. 앨런 튜링. 노벨상은 다들 아실 거고, 수학의 노벨상은 보통 ‘필즈 메달’을 이야기하죠. 컴퓨터 과학의 노벨상은 ‘튜링상’입니다. 그만큼 앨런 튜링은 오늘날 컴퓨터와 인공지능의 아버지로 평가를 받고 있죠.
2차대전 당시 미국 프린스턴연구소에서 연구하고 있던 앨런 튜링은 고국이었던 영국이 전쟁에서 불리해지자 블레츨리 파크라고 하는 암호정보기관으로 가죠. 여기에서 그는 난공불락의 독일군 암호 ‘에니그마’를 컴퓨터와 확률을 이용해서 해독해 냅니다. 그래서 앨런 튜링은 컴퓨터 과학의 아버지이기도 하지만, 처칠, 루즈벨트보다 위대한 2차대전의 진짜 영웅으로 평가받고 있죠.

그런데 컴퓨터로 암호를 해독했다는 건 어느 정도 알겠어요. 도대체 확률적으로 해독했다는 말이 뭘까요? <여기에 빈칸이 있습니다. 이 빈 칸에는 16개의 알파벳 중 어느 하나를 랜덤으로 집어넣습니다. 이때 이 알파벳이 아닐 확률은 얼마죠?> 당연히 1/26입니다. 그런데 ‘빈칸 앞에 E가 있다’라고 할 때 ‘R’이 나올 확률은 얼마죠? 영어 단어에서 E하고 R이 같이 나오는 경우가 매우 많아요. very, hamburger, lover. 이와 같이 암호를 풀 때 각 칸에 들어간 알파벳이 항상 26분의 1은 아닌 거죠. 문장의 구조에 따라서 앞 단어에 따라서 확률은 매번 달라지는 것입니다.
수학적 사고, 내 관점이 달라지는 계기
혹시 넷플릭스 보시나요? 여러분의 넷플릭스 초기 화면과 제 초기화면 매우 다를 수 있습니다. 만약에 30대 어떤 여성이 매번 로맨스코미디 장르만 봤다고 칩시다. 이분의 넷플릭스 초기 화면에 <서울의 봄>이 떠 있을 확률은 많이 없죠. 이는 자율주행이 매순간 그때그때 따라서 도로의 확률을 바꾸는 것과 똑같습니다. 넷플릭스에서는 이걸 추천 알고리즘이라고 하죠. 넷플릭스가 OTT의 제왕이 된 핵심은 창업자인 리드 헤이스팅스가 수학 전공자거든요. 이 분이 처음에는 비디오 가게, DVD 대여점으로 출발합니다. 자기가 비디오를 빌리고 까먹고 반납을 안 하다보니까 자꾸 연체료와 쌓여서 자기 자신한테 화가 났던 거죠. 그래서 이 대여점의 정책은 ‘연체료를 안 받는 정책’이었습니다. 대신에 고객은 개인정보와 DVD를 반납할 때 평점을 제출해야만 했죠. 이 데이터들을 통계적으로 분석을 해서 작은 대여점이었던 넷플릭스는 고객들에게 DVD를 추천해주기 시작하죠. 이게 진화하여 추천 알고리즘이 되었다는 사실! 이 정도면 왜 수학이 중요한지 아시겠죠?

모든 사람이 수능 30번을 풀고, 리만 가설에 도전해야 되는 건 전혀 아닙니다. 하지만 분명한 건 경험적 세계 안에서 살아가는 사람과 수학적 사고관을 가지고 선험적인 능력을 가진 사람은 인생의 성과가 다를 수밖에 없죠.
그런 관점에서 저는 수학, 과학의 역사를 아는 게 무엇보다 중요하다고 생각합니다. 수학을 잘하기 위해서 수학자들이 어떤 삶을 살았는가를 아는 것도 중요하지만, 그들이 어떤 사고를 했고 어떤 식으로 생각해서 문제를 해결했는가? 아까 뉴턴처럼 이런 것들을 이해하는 것은 우리가 앞으로 수학을 잘하고 수학을 일상에서 유용하게 사용하는데 큰 도움이 될 것입니다.
원문출처 : https://knou-oun.tistory.com/entry/%EC%9A%B0%EB%A6%AC%EA%B0%80-%EC%88%98%ED%95%99%EC%9D%84-%EB%B0%B0%EC%9A%B0%EB%8A%94-%EC%9D%B4%EC%9C%A0



